How do Mechanical Calculators count. An technological overview

Below the English names and alternative names, as well as the German names for these technologies:

Direct add ; rocker arm or switching wing (key driven) or Schaltschwinge (DL)
Rocking Segment or oscillating tooth bars(UK), Zahnsegment or Zahnstange(DL)
Pin-wheel (UK), Sprossenrad (DL)
Stepped Drum or Leibnitz wheel (UK), Staffelwalze (DL)
Proportional Lever (UK), Proportionalhebel (DL)
Switching Latch Wheel (UK), Schaltklinke (DL)

By the direct add, the value of the key is direct added to the corresponding digit, of the result register. Very fast adding was possible.
At the Rocking Segment technology, the numbers has to be inputted on the key board, followed by pulling a reciprocating handle. The same for the next numbers. Total or subtotal keys has to pressed and followed by the handle pulling to. That made it successful in the adding and listing and bookkeeping machines. The lowest two technologies of the overview, came from the drawing board of Mr. C. Hamann an Icon in mechanical calculator history. These clever technologies played an important role in calculation automation. In fact the last four technologies have rotating or crank type actuators, which is good for rapid and repeating cycles. That made them suitable for automation. Although it is a sole used technology I like to mention the Marchant Silent Speed Proportional Gears technology used in their Figurematic 8ADX for instance. An other technology used by a few manufacturers, is the Adapting Segment technology, which is used in Marchants LX and H8 machine, the Demos and the EOS.
Further on on this page we will see a one cycle way of multiplication a very interesting method but became no successor.

Beside this subdivision of mechanical calculator technologies, you will find an other qualification, the number of arithmetic functions, which can be performed. This is often used in Germany. The machines, who can easily add or add and subtract only, are called "Ein or Zwei Spiezies Rechenmaschinen" (DL). Machines who could easily perform multiplications or multiplications and divisions as well are called "Drei and Vier Spiezies Rechenmaschinen"(DL) *)2.
So lets combine those two and we will get a performance overview:

*Technology*	*Can be used for:*
Direct add	Add, Subtract with nine complement.
Rocking Segment	Add and some can Subtract *)1
Pin-wheel	Add, Subtract, Multiply and Divide
Stepped drum	Add, Subtract, Multiply and Divide *)2
Proportional Lever	Add, Subtract, Multiply and Divide in a automatic sequence
Switching Latch Wheel	Add, Subtract, Multiply and Divide in a automatic sequence

The best technology. Often the question is raised: "What is the best technology?". Let me tell you, it is almost impossible to answer this. The searches after new possibilities off calculating, was not only a battle of "who is the best", but as well how can I build a mechanism for calculating without using the patented technologies of other manufacturers. How can we be different?

*1) No doubt that the last four technologies are the ones for multiplication and divide for large numbers and great precision (12 digits and more). But for relative small precisian numbers (4 to 6 digits), the ten key Rocking Segment machines are the exception on the rule. As you will see on the chapter of the Rocking Segment technology.
*)2 There are very seldom machines, fi the Friden RWS10, who can take automatically square roots as well, this Calculator is a "Funf Spiezies machine" (DL).

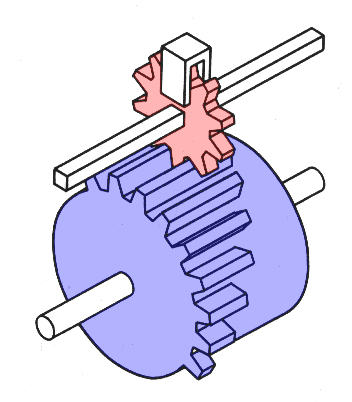
Concluding observations (How do they calculate, introduction part)
When we have worked ourselves through all these technological details, I think is good to summarize this chapter:
Many people, in previous ages, worked on improving mechanical calculating machines. Those machines displays the results either on printed paper or numbered (0 .. 9) rounds, mounted on the side of gearwheels. One round for every digit. They form the registers of the machine. The way those gearwheels get turned, for instance during an adding, can be grouped by and are named after, the essential part of the automation / the calculation technology.
We saw that the keyboards and sliders are used for the inputting the figures by hand. These input mechanisms converts a given figure into a corresponding distance or a corresponding number of pins, stick out of a wheel. During the calculation activation, by hand or motor, those keyboard conversions on their turn are converted into equivalent teeth turning of the result gearwheel / register. We saw that the tens-carry is mostly carried out at mechanisms close to the registers and that machines with a movable carriage are, at the beginning of the mechanical calculator era, the best suitable for multiplication and division.

I like to recommend opening these links:

The last one is on the John Wolff's Web Museum (Melbourne). The complete set-up of the Millionaire. I like to recommend reading this one, when you think you are good at repairing mechanics. My belief this work is compared to none!! His work was and is still of great help for collectors like I am.

repetitive additions with shifted carriage etc. There is however a small group of mechanical calculators which where able to performed a direct multiplication. Meaning that they perform a multiplication in only one machine cycle (digit for digit of the multiplier). Those machines make use of a Multiplying Body (Multiplications Körper (DL)). Two examples of the Otto Steiger developed ones, on pictures to the right. The first one has to turn and shift to get in position, the lower one has to shift horizontal and vertically.
It is not clear who had invented this method, some documents give the credits to Russian mathematician "Pafnuty Lvovich Chebyshev (1881)", he put his ideas in a few prototypes, but no machines build for the market.
Leon Bollee however is known for the first direct multiplier machine (1889) using a multiplying body and you might see his machine as the ancestor of the Millionaire, the machine developed by Otto Steiger (1893). This millionaire machine was solid enough for mass production. The multiplying body he finally used, is showed right / below.
(Please see the John Wolff web museum for more detailed explanations and very nice pictures)

The principle

When we like to perform a multiplication, of for instance 7 x 6 = 42, we have to change the result register differently than we did with an add. At an adding a carry to the next digit, is maximum one unit. We now have to change the next digit, in our example, with 4 units. And of course the actual digit with two units, in this example.
What if we had a block with two pins of exactly the length of 4 and 2 units?
We could shift a tooth rack against it and on the way back put the result register on the rack and get the result 42. The picture below show the real thing and more digits. Please see the drawing below.

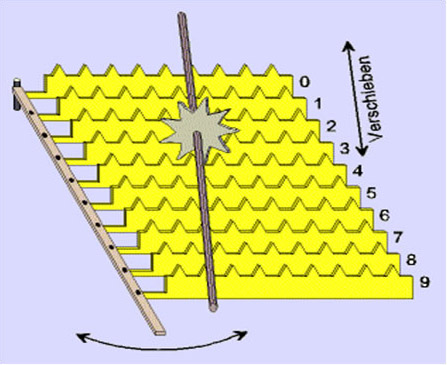
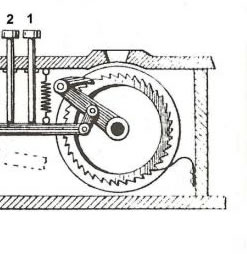
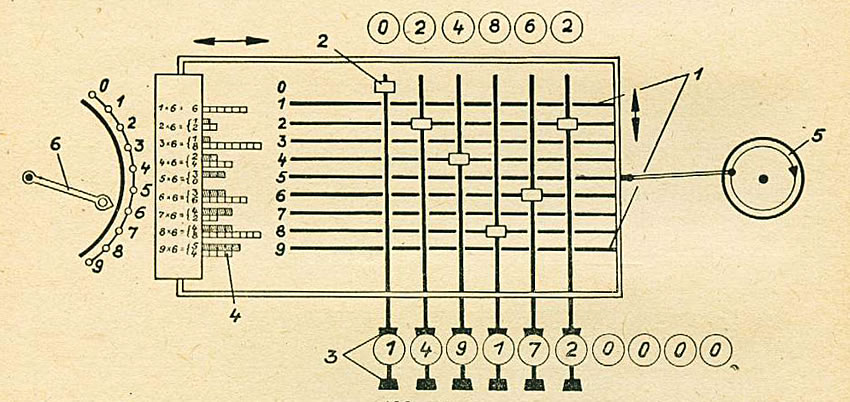
This is the principle of the direct multiplication with a multiplying body (no 4 on the drawing). Instead of only two pins this body has an array of pin sets, where all results of 1x1 till 9x9 are in an row / column configuration. So two pins with the length from 0,1 till 8,1 for each combination / result.
The multiplying body can vertically shifted / tiled to have the exact row (y position of the array) of the multiplier (6 in the drawing above). This by setting the crank no 6. The number to be multiplied (max 8 digits) can be set by sliders no 2. They set the x positions of the multiplying body.
A second turn on the wheel no 5 and a shift of the multiplying body is needed to process the tens carry's, as said this is often more than one unit.(The crank who drives the wheel 5 has a 1 to 2 gear up, so that the crank has only one turn / multiply)

The initial success of the machines was declining due to the:
- the one digit per machine cycle of one of the multiplying numbers
- difficult division
- automats, who came on the market with full automation of multiplication an division.

An other direct multiplication machine was developed by Mr. Moon Hopkins in 1911 in St. Louis. Burroughs marketed this machine under Class 7 in 1921.

The drawing above is taken from the Rechenlexicon / Wittke 1948 Die Rechenmaschine und ihre Rechentechnik
A nice document on the subject is from Ullrich Wolff ( ARITHMEUM in Bonn )
An other pioneer working on direct multiplication was Edmund Barbour (1872) Boston, Massachusetts USA